4.1 二维曲线
plot函数
- 基本用法:
plot(x,y),x和y分别代表横纵坐标,plot函数会将各个点连接起来,形成线,x和y一般为长度相等的向量。 - 最简单的调用格式:
plot(x)- 当x为实向量时,则以该元素下表为横坐标,元素的值为纵坐标绘制曲线。
- 当x为复向量时,则以实部和虚部分别为横纵坐标绘制曲线。
- plot(x,y)函数参数的变化形式
- 当x为向量,y为矩阵:这时x的长度和y的列数(或行数)必须相等。这时候绘制多条曲线,分别是x为横坐标,取与x长度相等的那一个参数作为纵坐标,另一个参数为曲线的条数。如果y的行、列两个参数相等,那么用y的每一列作为纵坐标,曲线条数等于矩阵列数。
- 当x和y为同型矩阵:这时以x,y对应列元素为横、纵坐标绘制曲线,曲线条数等于矩阵列数。
- 含多个输入参数:形如
plot(x1,y1,x2,y2,···,xn,yn),那么就是以每一个向量对组成一个点,绘制曲线。
- 含选项的plot函数,plot(x,y,选项)
- 线型 :通过
"-",":","-.","--"等参数来实现实线,虚线,点画线,双画线。 - 颜色 :通过
"r","g"等实现曲线颜色的切换。当颜色选项省略,绘图自动循环使用。 - 数据点标记 :通过
"*","o","s"等来实现将数据点用星号,圆圈,方块标记。
- 线型 :通过
fplot函数
可根据参数函数的变化特性自适应地设置采样间隔,当函数值变化缓慢,采样间隔大,当变化快的时候,采样间隔小。
基本用法:
fplot(f,lims,选项),参数分别函数(一般采用函数句柄表示),lims为x轴的取值范围,采用二元向量[xmin,xmax]来表示,默认值为[-5,5]。选项参数与plot函数相同。双输入参数函数的用法:
fplot(funx,funy,tlims,选项),前两个分别为x,y的参数表示,通常以函数句柄的形式给出。tlims为前方函数参数 t 的取值范围,用二元向量[tmin,tmax]表示,默认的值为[-5,5],选项参数与上述相同。
例程
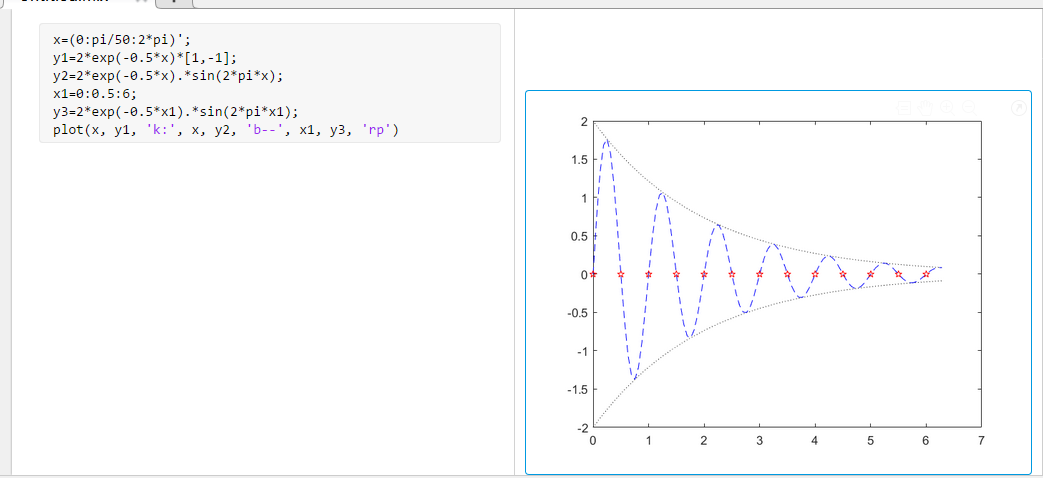
- 利用不同的线型和颜色在同一坐标内绘制曲线 $y=2e^{-0.5x}sin(2\pi x)$ 以及其包络线。(包络线:在几何学,某个曲线族的包络线(Envelope),是跟该曲线族的每条线都有至少一点相切的一条曲线。)
x=(0:pi/50:2*pi)';
y1=2*exp(-0.5*x)*[1,-1]; %这里绘制的是上下两条包络线,是有两行的矩阵。
y2=2*exp(-0.5*x).*sin(2*pi*x); %这里绘制的是曲线本身
x1=0:0.5:6;
y3=2*exp(-0.5*x1).*sin(2*pi*x1); %这里标记的是正弦函数和x轴的交点。
plot(x, y1, 'k:', x, y2, 'b--', x1, y3, 'rp')
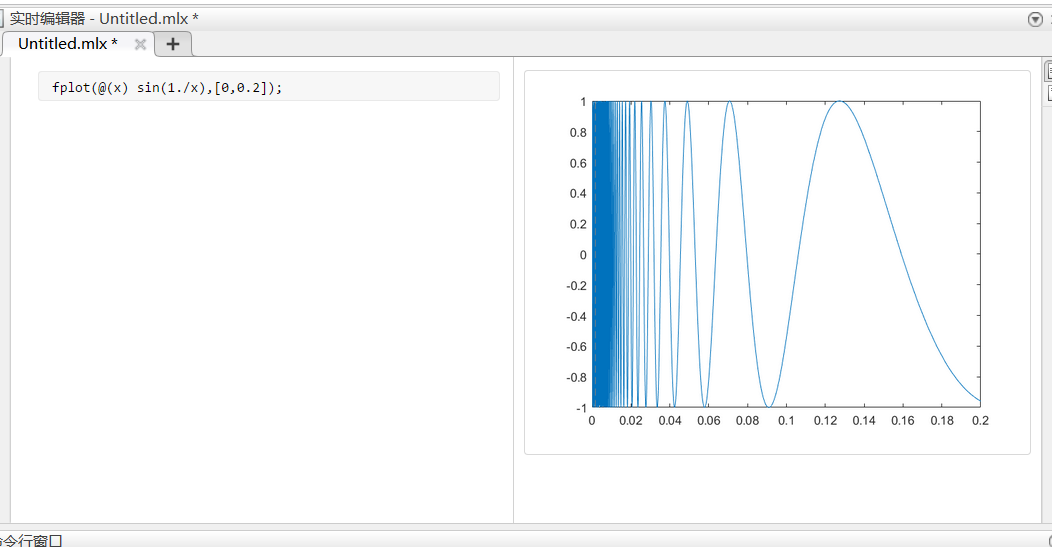
- 利用fplot函数绘制 $y=sin{\frac{1}{x}}$ 在区间 $[0,0.2]$ 的图像。
fplot(@x sin(1./x),[0,0.2])
4.2 绘制图形的辅助操作
添加图形标注
title函数:用于给图形添加标题说明
- 基本用法:
title('图形标题'),如果是有多行,就用逗号分隔,大括号{}括起来。 - LaTeX排版:可在在图形标题中使用LaTeX格式控制符,要用LaTeX时将其控制字符用大括号
{}括起来。 - 控制字体:用
"\bf","\it","\rm"分别控制字体加粗,斜体以及正体。 - 设置title函数属性 :
title(图形标题,属性名,属性值)其中属性名和属性值对应成对出现。- Color属性:用于设置图形标题文本的颜色,缺省时为黑色。
- FontSize属性 :用于设置标题文字字号,缺省时为11。
- 基本用法:
xlable和ylable函数:给x轴和y轴添加说明
- 基本用法:
xlable(x轴说明),ylable(y轴说明),同样还有 zlable等。
- 基本用法:
text函数和gtext函数:给特定位置说明
- 基本用法:
text(x,y,说明),x、y参数用来指明说明的位置,后面的说明和title函数类似。gtext(说明)这里没有坐标指定位置,通过鼠标的点击来指定位置。
- 基本用法:
legend函数:用于给图形添加图例
- 基本用法:
legend(图例1,图例2,···)其中图例顺序要与plot函数中参数顺序相对应,图例的说明方式与tiele函数标题说明类似。
- 基本用法:
坐标控制
axis函数:用于设置坐标轴的范围
基本用法:
axis([xmin,xmax,ymin,ymax,zmin,zmax]),分别代表了x,y,z轴范围。其他用法:通过在axis函数下面加语句来实现控制其他格式。
- axis equal:横纵坐标刻度等长。
- axis square:采用正方形坐标系(默认为矩形)。
- axis auto:使用默认设置。
- axis off/on:不显示/显示坐标轴。
给坐标系加网格和边框
- 添加网格:通过
grid on/off控制显示和不显示网格线,而直接用grid用于切换两种形式,如果是带网格则切换为不带,反之亦然。如果不添加语句,则默认不带。 - 添加边框:通过
box on/off控制显示不显示边框,用法与 grid 类似,如果不添加语句,则默认带网格。
- 添加网格:通过
图形保持
一般情况下绘图命令每执行一次,图形界面就刷新一次,去掉原有图形,绘制新图形,如果要保留原有图形,可使用图形保持命令。通过hold on\off 来控制是否保留,通过 hold 切换保留和不保留两种选择。
图形窗口分割
- 子图:同一图形窗口中的不同坐标系下的图形称为子图。
- subplot函数 :
subplot(m,n,p)意思是将图形窗口分成 $m\times n$ 个子图区域,当前绘制的是第p个子图,区号按行编号。我们在一个图形窗口内,绘制不同的图可以采用不同的分割。
例程
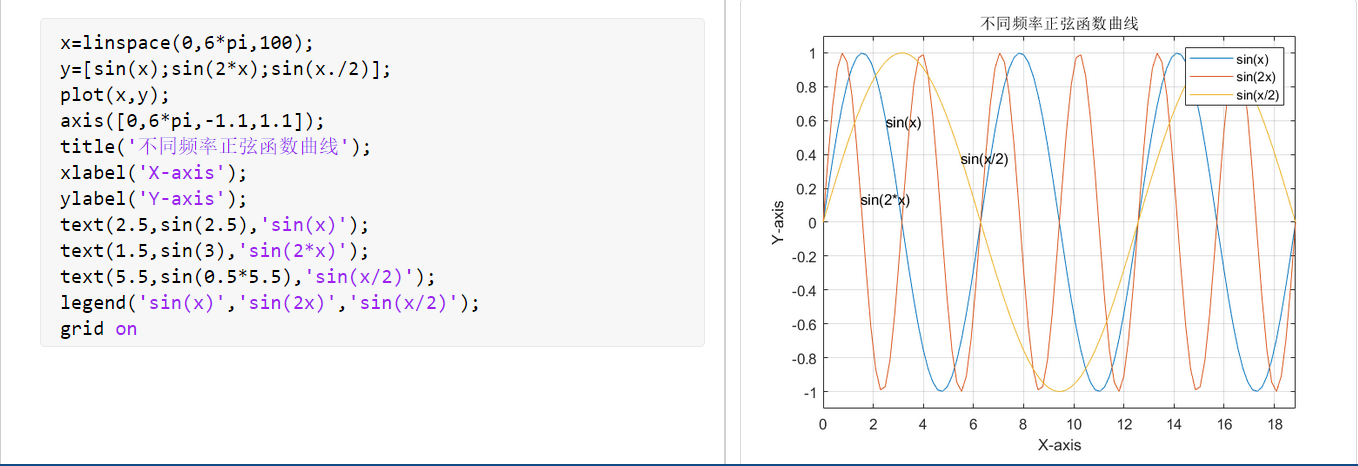
- 绘制 $sinx$ 、$sin2x$ 、$sin(\frac{x}{2})$ 的图像,并添加相应的图形标注。
x=linspace(0,6*pi,100);
y=[sin(x);sin(2*x);sin(x./2)];
plot(x,y);
axis([0,6*pi,-1.1,1.1]);
title('不同频率正弦函数曲线');
xlabel('X-axis');
ylabel('Y-axis');
text(2.5,sin(2.5),'sin(x)');
text(1.5,sin(3),'sin(2*x)');
text(5.5,sin(0.5*5.5),'sin(x/2)');
legend('sin(x)','sin(2x)','sin(x/2)');
grid on
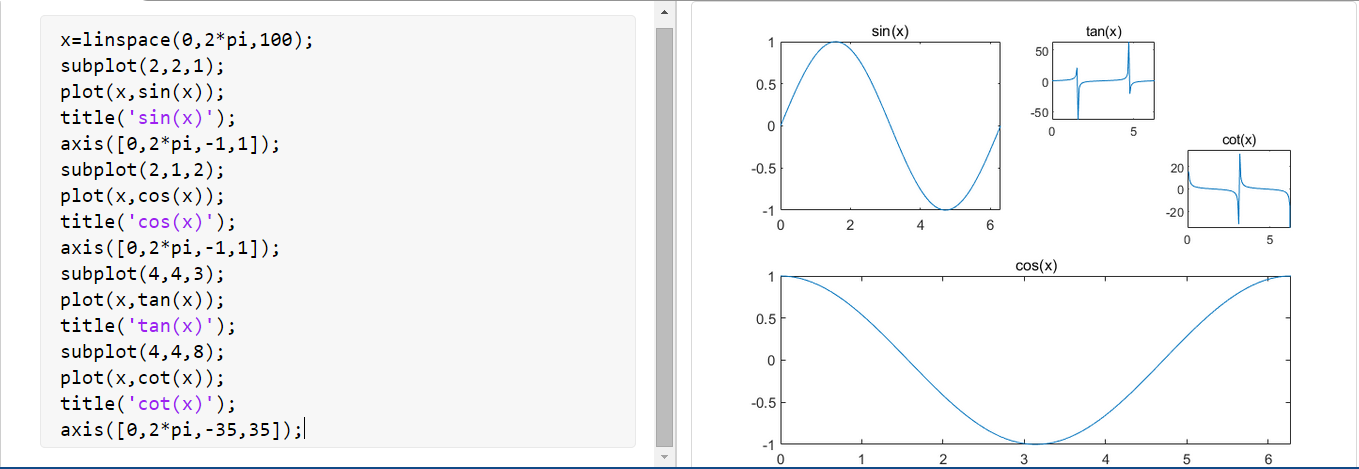
- 利用子图函数在不同区域绘出不同图形。
x=linspace(0,2*pi,100);
subplot(2,2,1);
plot(x,sin(x));
title('sin(x)');
axis([0,2*pi,-1,1]);
subplot(2,1,2);
plot(x,cos(x));
title('cos(x)');
axis([0,2*pi,-1,1]);
subplot(4,4,3);
plot(x,tan(x));
title('tan(x)');
subplot(4,4,8);
plot(x,cot(x));
title('cot(x)');
axis([0,2*pi,-35,35]);
4.3 其他形式的二维曲线
其他坐标系下的二维曲线图
对数坐标图
- semilogx 函数:调用形式与plot函数类似,
semilogx(x,y,选项)为其中一种调用格式,其他的可参考plot函数,此函数绘图采用半对数坐标,x轴采用常用对数刻度,y轴为线性刻度。 - semilogy 函数:调用形式与plot函数类似,
semilogy(x,y,选项)为其中一种调用格式,其他的可参考plot函数,此函数绘图采用半对数坐标,y轴采用常用对数刻度,x轴为线性刻度。 - loglog 函数:调用函数与上述类似,x和y都为常用对数刻度。
- semilogx 函数:调用形式与plot函数类似,
极坐标图
- 基本调用格式:
polar(theta,rho,选项)theta为极角,rho 为极径,选项与plot函数类似。
- 基本调用格式:
统计图
条形类图形
条形图
bar 函数:绘制二维垂直条形图
- 调用格式为
bar(y,style):y如果为向量,则以每个元素值作为每一个柱的高度,元素下标代表横坐标。如果y为矩阵,则以每一行作为一组,以行号作为组号绘图。后方的 style 有"grouped"和"stacked"两种模式,分别为簇状分组和堆积分组。默认为簇状分组。 - 调用格式为
bar(x,y,style):其中x存储横坐标,y为矩阵,存储每一个横坐标对应的数据,y的行数必须与x的长度相对应。
- 调用格式为
barh 函数:绘制二维水平条形图。调用格式与bar函数相同。
直方图
hist 函数:绘制直角坐标系下的直方图。
- 调用格式为
hist(y),y为向量,绘图时将 $[miny,maxy]$ 区间等分成十组,并求出每个区间内对应元素的个数,然后绘出直方图。 - 调用格式为
hist(y,x),如果x为标量,则将y区间分成x个区间,如果x为向量,则向量中的每一个数指定分组的中心值,元素的个数为指定分成的组数,x缺省默认均分十组。
- 调用格式为
rose 函数:用于绘制极坐标系下的直方图。
- 调用格式为
rose(theta,x)其中参数 theta 用于确定每一数据与圆点的角度,如果x为标量,则x代表均分组数,缺省默认为20。
- 调用格式为
面积类图形
- 扇形图/饼图
- pie 函数:调用格式为
pie(x,explode)其中参数x为待统计的数据,通常为向量,其中每一个数据在整体中占用的比例在扇形图中表示出来,后续的 explode 为每个x对应的分离参数,如果非0,则将其分离出来。explode 缺省则饼图为一个整体。
- pie 函数:调用格式为
- 面积图
- area 函数:与plot函数类似,下方与坐标轴围成的区域进行填充。
- 扇形图/饼图
散点类图形
- 散点图
- scatter 函数:
scatter(x,y,选项,'filled'),其中x和y通常为同等大小向量,代表了一定数量的点。选项与plot函数类似,用于限制颜色,线型,以及数据点标记,如果采用数据点标记,则可以用 ‘filled’ 参数来填充数据点,如果缺省,则标记数据点为空心。
- scatter 函数:
- 阶梯图
- stairs 函数:使用方法与上述 scatter 函数类似。
- 杆图
- stem 函数: 使用方法与上述 scatter 函数类似。
- 散点图
矢量类图形
例程
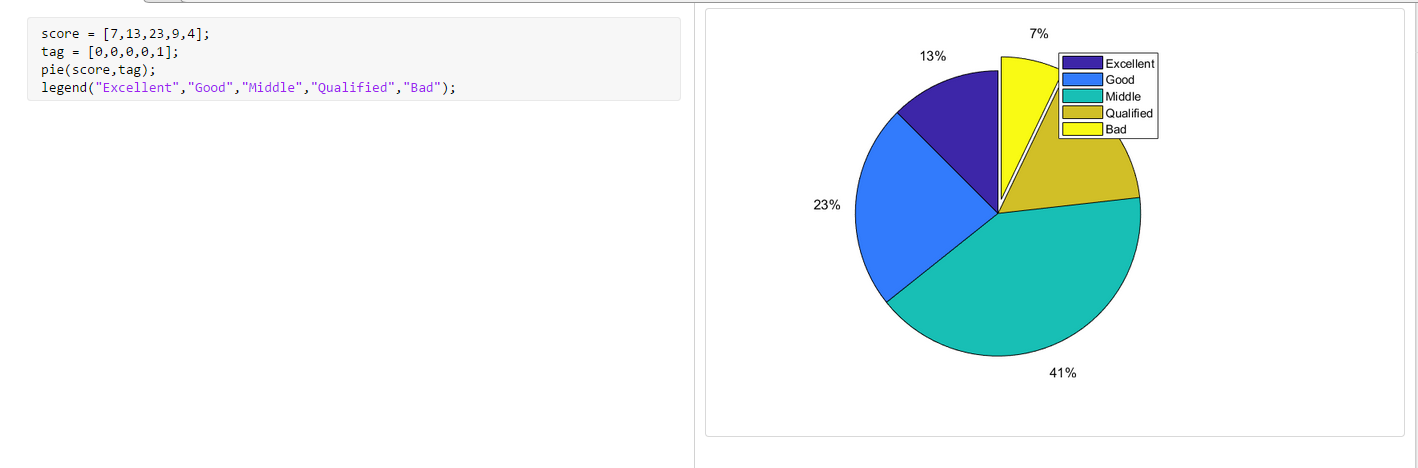
- 某次考试成绩优秀,良好,中等,及格,不及格人数分别为:7、13,23,9,4,用扇形统计图作成绩统计。
score = [7,13,23,9,4];
tag = [0,0,0,0,1];
pie(score,tag);
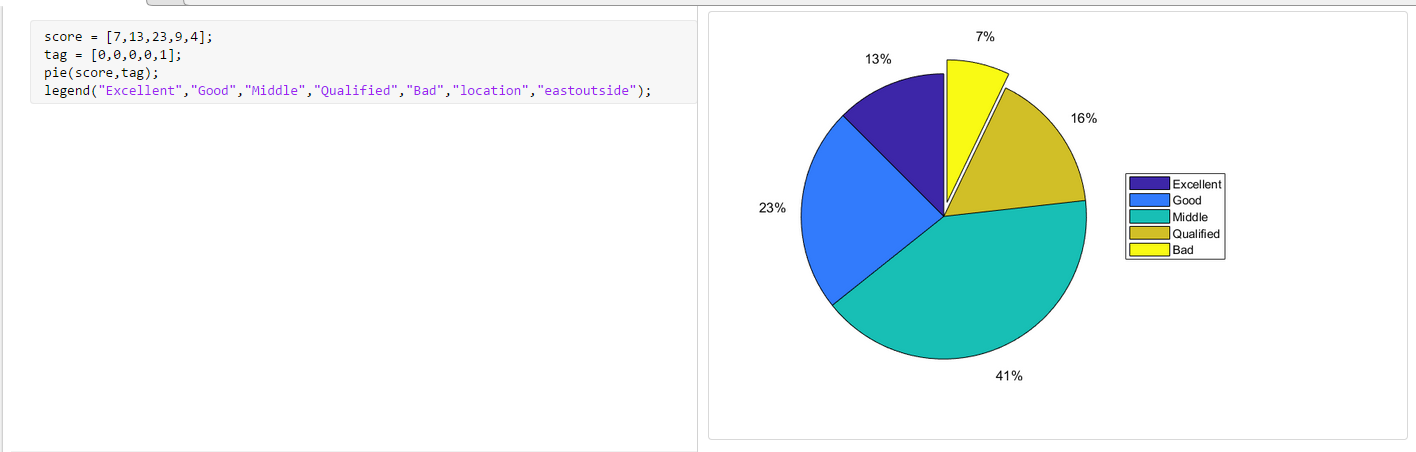
legend("Excellent","Good","Middle","Qualified","Bad",'Location','eastoutside');
%上方legend中的location是用于指定图例出现位置的,如果不指定,会与统计图重合
不加location参数
加入location参数
4.4 三维曲线
plot3函数:绘制三维曲线最常用的函数。
基本用法:
plot3(x,y,z)其中三个参数分别为坐标对,一般为等长向量,plot3函数用直线将所有点连起来。变化形式:
当
plot(x,y,z)当x,y,z为同型矩阵,则绘制多条曲线,曲线条数等于矩阵列数。当x,y,z中有向量也有矩阵的时候,向量的长度应与矩阵相符,如果是行向量,那么行向量的长度应与矩阵列数相同,如果是列向量,那么列向量的长度应与矩阵行数相同。
也可以用多组向量对来绘制多组曲线,
plot(x1,y1,z1,x2,y2,z2···,xn,yn,zn);
含选项的plot3函数:
plot(x,y,z,选项)选项与功能与plot函数类似。
fplot3函数
- 基本用法:与fplot函数类似
4.5 三维曲面
生成平面网格数据
- meshgrid 函数:调用格式
[X,Y]=meshgrid(x,y),其中x,y为向量,X,Y为存储网格坐标系横纵坐标的矩阵。如果只填一个 x ,那么就相当于 x=y 。
绘制三维曲面的函数
mesh 函数 & surf 函数
基本调用格式:
mesh(x,y,z,c) & surf(x,y,z,c),两者可以用来绘制三维曲面,其中x,y为网格坐标矩阵,z 是网格点上的高度矩阵,c 用于指定在不同高度下的曲面颜色。如果 c 缺省,则默认 c=z ,也就是说颜色正比于高度。其他调用格式:
mesh(z,c) & surf(z,c)这样的话就用z矩阵的列,行坐标代表x,y的值,z的值代表高度,c的意义与上面相同。其他花里胡哨的 :
- 带等高线的三维网格曲面函数
meshc和 带底座的三维网格曲面函数meshz,用法与 mesh 函数相同。前者带等高线,后者带底座(就是说下面是实体的)。 - 带等高线的曲面函数
surfc和具有光照效果的曲面函数surfl。
- 带等高线的三维网格曲面函数
标准三维曲面
- sphere 函数:生成三维球面对应坐标。格式
[x,y,z]=sphere(n),这将产生x,y,z三个(n+1)阶的方阵,通过这三个方针结合绘制三维曲面的函数 (surf或者mesh),可以绘制出圆心在圆点,半径为一的单位球面。如果不加输出参数x,y,z,则直接绘制球面。n的值代表圆滑程度,默认为20. - cylinder 函数:生成三维柱面对应坐标。格式为
[x,y,z]=cylinder(R,n)R为一个向量,存放柱面各个等间隔高度上的半径,n表示圆柱圆周上的间隔点个数,默认为20。如果R为标量,则生成一个柱面。
fsurf和fmesh函数
用于绘制参数方程表示的函数,并且有两个变参。调用格式为 fsurf(funx,funy,funz,uvlims),其中前三个通常为函数句柄形式给出的函数,uvlims 表示前三个函数自变量取值范围,用四元向量组来进行描述,形如[umin,umax,vmin,vmax],默认值为[-5,5,-5,5] 。
例程
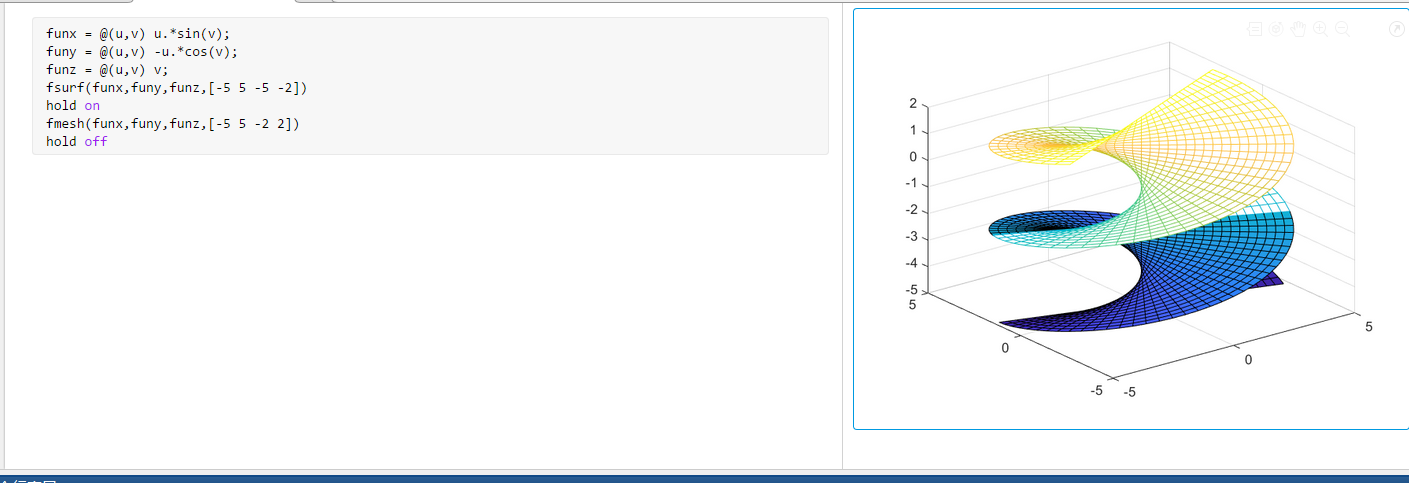
- 绘制螺旋曲面。
funx = @(u,v) u.*sin(v);
funy = @(u,v) -u.*cos(v);
funz = @(u,v) v;
fsurf(funx,funy,funz,[-5 5 -5 -2])
hold on
fmesh(funx,funy,funz,[-5 5 -2 2])
hold off
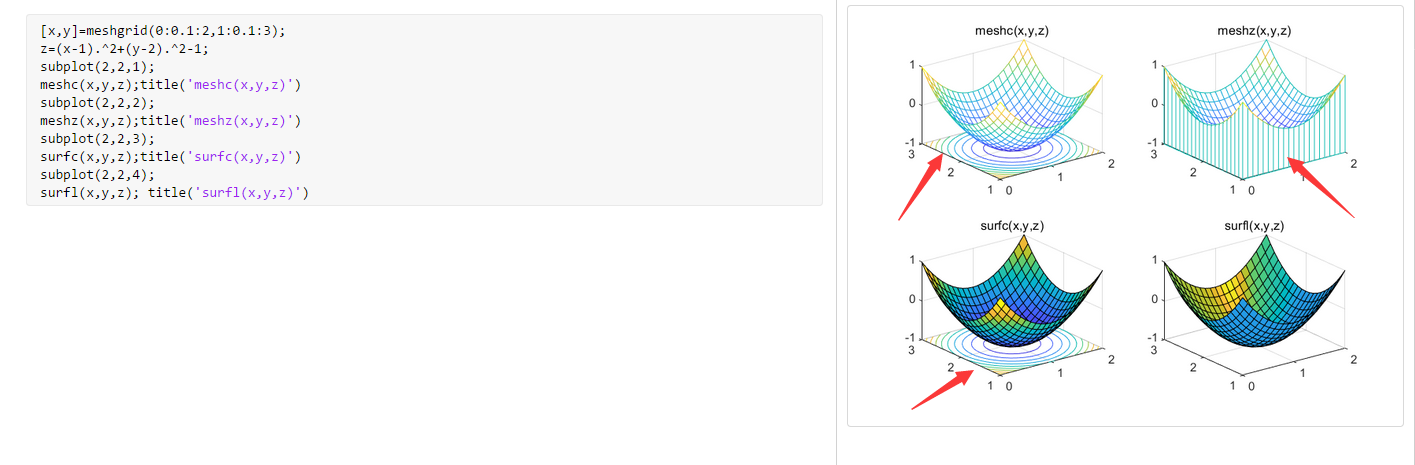
- 绘制函数$z=(x-1)^2+(y-2)^2-1$ 的曲面图,分别用带等高线的mesh函数,带底座的mesh函数,带等高线的surf函数,带光照效果的surf函数绘制。$x\in[0,2],y\in[1,3]$
[x,y]=meshgrid(0:0.1:2,1:0.1:3);
z=(x-1).^2+(y-2).^2-1;
subplot(2,2,1);
meshc(x,y,z);title('meshc(x,y,z)')
subplot(2,2,2);
meshz(x,y,z);title('meshz(x,y,z)')
subplot(2,2,3);
surfc(x,y,z);title('surfc(x,y,z)')
subplot(2,2,4);
surfl(x,y,z); title('surfl(x,y,z)')