专题一:MATLAB基础知识

1.1 MATLAB系统环境

MATLAB操作界面的组成

MATLAB主窗口
命令行窗口
- 命令行窗口含有 >> 命令提示符，表示MATLAB处于准备状态，可以接受并执行命令，按下回车键后MATLAB会执行输入命令，并在后面显示执行结果
- 如果指令过长可以分行输入，在一行末尾写 ... 并按下回车键，在下个命令行继续输入，...称为续行符。
当前文件夹窗口
- 在MATLAB编程过程中生成的文件自动存放在当前文件夹，我们可以通过cd命令(例如我们要进入E盘下的work文件夹，可以cd e:\work)或者选择文件工具栏中的文件夹来设置当前文件夹。
工作区窗口
- 可用于变量的显示和操作，可显示你当前创建的变量。并且可对其保存，修改，删除。

MATLAB的搜索路径

检索命令对象的顺序如下

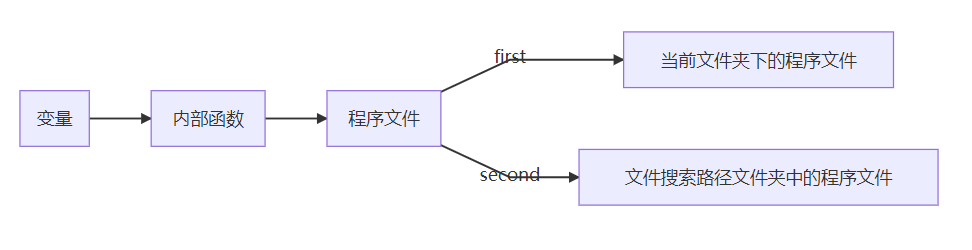
设置文件搜索路径
- 用path命令设置文件搜索路径。例如： path{path,`e:\work`}
- 用对话框设置文件搜索路径。在MATLAB主窗口的主页中设置。

1.2 MATLAB数值数据

数值数据类型的分类

整型
- 无符号整数：含有8，16，32，64四种
- 带符号整数：含有8，16，32，64四种
范围和C语言一样,通过类型(数据) 来进行强转。
浮点型
- 单精度：占四字节
- 双精度：占八字节，数值数据默认为双精度
通过single和double函数进行强转。
复型
- 复型数据包括实部和虚部两部分，都默认为浮点型，虚数单位用i或j来表示。
- 通过read和imag函数来求复型数据的实部和虚部。
字符型
- 字符在内部作为数字存储，而不会采用浮点格式存储。

数值数据的输出格式

format命令的格式，使用方法 format 格式符，不带格式符的format会恢复默认格式。ps：format只影响数据的输出，不影响数据的存储和计算。

常用数学函数

函数的调用格式为： 函数名(函数自变量的值)
- 函数自变量规定为矩阵变量，也可以为标量（为矩阵的特例）。
- 函数在运算时将函数逐项作用在每个元素上，最后运算出来是一个与自变量同类型矩阵。
常用函数的应用
- 三角函数有两类，例如sin和sind两种，前面是弧度制，后面是角度制，其余cos等类似。
- abs函数可以求实数的绝对值、复数的模、字符串的ASCII码值。
- 用于取整的函数有fix，floor，ceil，round。分别为靠0取整，向下取整，向上取整，四舍五入取整。
- 判断是否为素数的函数isprime，是素数返回1，不是返回0。
```
>> x=[1:100];
>> k=isprime(x);
>> k1=find(k);
>> p=x(k1)

p =

  1 至 16 列

     2     3     5     7    11    13    17    19    23    29    31    37    41    43    47    53

  17 至 25 列

    59    61    67    71    73    79    83    89    97
```

1.3 变量及其操作

变量与赋值语句

变量本质是一个内存单元的抽象，变量名以字母开头，后接数字、字母或下划线，最多63个字符。
变量名区分字母大小写(case sensitive)，标准函数名以及命令名必须用小写字母。
赋值语句有两种格式
- 变量 = 表达式
- 表达式的值赋值MATLAB预定义变量ans
如果赋值后不加分号，会显示变量的结果，如果加了分号，则不显示。

预定义变量

预定义变量是系统自身定义的变量

ans 是默认赋值变量，命令行表达式值默认赋值给 ans
i 和 j 代表虚数单位
pi 表示圆周率
NaN 代表非数

变量的管理

变量的删除和修改

在工作区进行变量的删除和修改
- 通过 who 和 whose 命令来查看变量清单，前者只显示名称，后者显示各种信息

内存变量文件

用于保存MATLAB工作区变量的文件交内存变量文件，扩展名为.mat，也叫MAT文件，是一种二进制文件。
- save命令：创建内存变量文件，load命令：载入内存变量文件

1.4 MATLAB矩阵的表示

矩阵的建立

直接输入法建立矩阵
将矩阵的元素用中括号[] 括起来，按行输入元素，同一行元素用逗号或者空格分隔，用分号换行。

利用已有矩阵建立更大矩阵

个人感觉类似于分块矩阵，例子如下：

>> A=[1,2,3;4,5,6;7,8,9];
>> B=[-1,-2,-3;-4,-5,-6;-7,-8,-9];
>> C=[A,B;B,A]

C =

     1     2     3    -1    -2    -3
     4     5     6    -4    -5    -6
     7     8     9    -7    -8    -9
    -1    -2    -3     1     2     3
    -4    -5    -6     4     5     6
    -7    -8    -9     7     8     9

用两个实矩阵矩阵通过矩阵的运算可以建立复数矩阵，要确保两个矩阵同类型

>> B=[1,2,3;4,5,6];
>> C=[7,8,9;1,2,3];
>> D=B+i*C

D =

   1.0000 + 7.0000i   2.0000 + 8.0000i   3.0000 + 9.0000i
   4.0000 + 1.0000i   5.0000 + 2.0000i   6.0000 + 3.0000i

冒号表达式

通过冒号表达式可以产生行向量
一般格式为e1:e2:e3 分别是初始值，步长，终止值。可以省略e2，省略时步长为默认为1。

>> t=0:1:5
t=
	0	1	2	3	4	5
>> s=0:5
s
	0	1	2	3	4	5

通过linspace函数产生行向量
linspace(a,b,n) 代表首元素为a，末尾元素为b，产生n个元素，相应的，步长为(b-a)/(n-1)。当n可以省略，省略时默认n为100。

>> x=linspace(0,pi,5)
x=
	0    0.7854    1.5708    2.3562    3.1416

结构矩阵和单元矩阵

结构矩阵
- 类似于C语言的结构体，把很多个数据写成一个结构体，矩阵里的每个元素个元素都是结构体变量。给对应元素赋值格式为 结构体元素.成员名=表达式 。我们应该注意到，当一个结构体内没有我们赋值的成员，那么他会自动扩充矩阵来满足你的要求。
- 我们可以通过 s=struct('name',{'next','what'},'sex',{'male','unknow'}) 来创建一个包含 name 和 sex 两个成员的结构体。
单元矩阵
矩阵里的每个元素的类型可以不同，通过直接输入法建立，所有元素用大括号{}而不是中括号[]

1.5 矩阵元素的引用

矩阵元素的引用方式

通过下标来引用矩阵，例如A(3,2)表示A矩阵第三列第二个元素。如果我们引用的元素超出矩阵范围，那么会默认扩充矩阵至满足要求，拓展元素默认为0。

>> A=[1,2,3;4,5,6];
>> A(4,5)=10
A=
	1	2	3	0	0
	4	5	6	0	0
	0	0	0	0	0
	0	0	0	0	10

通过序号来引用，注意矩阵元素按列存储，依次存放第一列，第二列···最后一列。
矩阵元素的序号和下标可以通过 sub2ind 和 ind2sub 两个函数完成相互转化
- sub2ind 函数：将矩阵中指定元素的行列下标转换成存储的序号，格式为D=sub2ind(S,I,J)，三个参数依次为行数和列数组成的二维向量(可以通过size函数获取)，转换矩阵元素的行下标，转换矩阵元素的列下标。如果I，J为矩阵的话，那么就说明要将对应的一个下标矩阵求对应序号。注意结合下例来进行理解，我们注意到A(1,1)的序号为1，A(2,1)的序号为2，那么就是给定下标矩阵的顺序来生产的这个序号矩阵，类型相同。
```
>> A=[1:3;4:6]
A=
	1	2	3
	4	5	6
>> D=sub2ind(size(A),[1,2;2,2],[1,1;3,2])
D=
	1	2
	6	4
```
- ind2sub 函数：将矩阵元素的序号转换成下标，格式为 [I,J]=ind2sub(S,D) ，S,D分别为行数和列数组成的二维向量(可以通过size函数获取)，要获取下标的元素的序号(可以是一个向量，标志要获取多个元素的下标) ，那么前方的 I和J就是对应的行下标和列下标，类似于一个 sub2ind 函数的逆用。
```
>> [I,J]=ind2sub([3,3],[1,3,5])
I=
	1	3	2
J=
	1	1	2
```

利用冒号表达式获得子矩阵

我们可以用冒号表达式作为矩阵的行或列下标，也可以用单个:来当行或列下标，这代表取遍全部行或列。end运算符： 表示某一维的末尾元素下标。

A(i,:)	表示第i行的全部元素
A(:,j)	表示第j行的全部元素
A(i:i+m,j:j+m)	表示第i~i+m行和j~j+m列全部元素
A(i:i+m,:)	表示第i~i+m行全部元素
A(1:3;1:end) 这代表取1~3行和1~最后一列元素

利用空矩阵删除矩阵元素

空矩阵就是不含任何元素的矩阵，例如x=[] 就建立了一个空矩阵x。

>> C=[4,5,6;1,2,3]
C =

     4     5     6
     1     2     3
>> C(:,1:2)=[]
C =

     6
     3

改变矩阵的形状

通过reshape函数可以在矩阵元素个数不变的情况下改变矩阵形状，例如 reshape(A,m,n) 就是将A矩阵变成m行n列的矩阵，不改变矩阵元素的存储顺序，也就是依次按列存储，对应序号相同。

特殊的约定

通过指令A(:) 可以将所有元素堆叠成一个列向量，不改变存储顺序。

1.6 MATLAB基本运算

算数运算

基本算术运算：+(加)，-(减)，*(乘)，/(右除)，\(左除)，^(乘方)
- MATLAB的算数运算在矩阵意义下进行，单个数据运算是矩阵的特例。
- 加减运算
  - 两矩阵同型，对应元素相加减。不同型，发生错误。
  - 一个标量可以和矩阵进行运算，这时把标量对全体矩阵元素进行操作。
- 乘法运算
  - 很明显必须满足矩阵乘的条件，也就是当A*B时必须满足A的行数等于B的列数，此时称A，B矩阵是可乘的，或称两矩阵维数和大小相容。不相容就会发生错误
- 除法运算
  - 如果A是**非奇异矩阵(A的行列式不为0) **,则B/A等效于B*inv(A)，A\B等效为inv(A)*B。inv(A)是指A的逆阵 。
- 乘法运算
  - A矩阵的x次方可以表示成A^x ，要求A为方阵，x为标量。
点运算
- 点运算符：在相应算术运算符前面加.，有点乘，点右除，点左除，点乘方。
- 点运算：两个同型矩阵对应元素进行相关运算。
```
>> A=[1,2;3,4];
>> A^2  
ans =

     7    10
    15    22

>> A.^2
ans =

     1     4
     9    16
```

关系运算

关系运算符： < ，<=，>，>=，==(等于)，~=(不等于)
两个比较量为标量，直接比较两个数大小，如果成立表达式值为1，否则为0。
如果两个矩阵是同型矩阵，对每两个对应元素进行比较，形成一个由0，1构成的同型矩阵。
如果一个是标量一个是矩阵，则用标量和每个矩阵元素比较，形成一个同型矩阵。

逻辑运算

逻辑运算符： &(与)，|(或)，~(非)。各自对应的运算法则和C语言类似，不再赘述。
标量，矩阵之间进行运算，对应规则和关系运算类似，不再赘述。

运算符的优先级

算术运算优先级最高，逻辑运算优先级最低，但是逻辑非运算是单目运算符，优先级比双目运算符高。

1.7 字符串处理

字符串的表达

用单引号括起来的字符序列就是字符串，MATLAB把他当成一个行向量。若字符串中含有单引号，则单引号字符要用两个单引号表示。
可以建立多行字符串，建立字符矩阵**（注意每一行的字符串长度要相等）**。和数值矩阵无异。

字符串的操作

字符串的执行
- 通过eval(s) 函数可以执行字符串 s 对应的命令行命令。
字串与数值之间的转换
- abs 和 double 函数都可以获取字符串矩阵对应的ASCII码矩阵。
- char 函数可以把ASCII码矩阵转换成字符串矩阵。
字符串的比较
- 关系运算符比较：两个等长字符串比较，两两对应字符比较，成立为1，不成立为0，得到是一个含0，1的行向量。
- 字符串比较函数比较
  - strcmp(s1,s2)：比较s1和s2是否相等，返回值为一个标量，相等为0，不等为1。后缀加i表示比较时忽略大小写。
  - strncmp(s1,s2,n)：比较s1和s2前n个字符是否相等，返回值为一个标量。相等为0，不等为1。后缀加i表示比较时忽略大小写。
字符串的查找和替换
- findstr(s1,s2)：返回短字符串在长字符串中的开始位置。如果出现多次，则返回一个行向量。
- strrep(s1,s2,s3)：将s1中所有子字符串s2替换为s3。
数值转换为字符
- 通过 num2str 或 int2str 等函数可以将数字转换为字符

1.1 MATLAB系统环境#

MATLAB操作界面的组成#

MATLAB的搜索路径#

1.2 MATLAB数值数据#

数值数据类型的分类#

数值数据的输出格式#

常用数学函数#

1.3 变量及其操作#

变量与赋值语句#

预定义变量#

变量的管理#

1.4 MATLAB矩阵的表示#

矩阵的建立#

冒号表达式#

结构矩阵和单元矩阵#

1.5 矩阵元素的引用#

矩阵元素的引用方式#

利用冒号表达式获得子矩阵#

利用空矩阵删除矩阵元素#

改变矩阵的形状#

特殊的约定#

1.6 MATLAB基本运算#

算数运算#

关系运算#

逻辑运算#

运算符的优先级#

1.7 字符串处理#

字符串的表达#

字符串的操作#

1.1 MATLAB系统环境

MATLAB操作界面的组成

MATLAB的搜索路径

1.2 MATLAB数值数据

数值数据类型的分类

数值数据的输出格式

常用数学函数

1.3 变量及其操作

变量与赋值语句

预定义变量

变量的管理

1.4 MATLAB矩阵的表示

矩阵的建立

冒号表达式

结构矩阵和单元矩阵

1.5 矩阵元素的引用

矩阵元素的引用方式

利用冒号表达式获得子矩阵

利用空矩阵删除矩阵元素

改变矩阵的形状

特殊的约定

1.6 MATLAB基本运算

算数运算

关系运算

逻辑运算

运算符的优先级

1.7 字符串处理

字符串的表达

字符串的操作